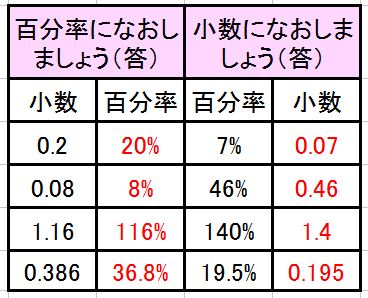
割合の学習の過程では、こんなことは確実にできるようなっていないと話にならない。徹底する部分とそうでない部分は分けて捉える。
小学校5年算数「割合」の問題は普通に教えても理解できない!?算数で難しいと感じている割合の問題!小学生を苦しめています(笑)
そもそも算数の教科書の説明がそれなりに難しくて、読んでわかる子どもは非常に少ないです。
ですから、教師が色々と工夫しますが、勉強苦手な子はなかなか理解できないのが割合です。
もとにする量、比べられる量、割合という三つの用語が出てきますが、これがまずもってなんだか見当が付きにくいものですね。はじめにこれが出てくるのですが、苦手な子は何それ?って感じです。
もっと簡単に教えることができないか?
全てを理解できなくてもいいから、割合って何なの?っていうことで、算数の苦手な子どもたちに最終的にこれだけわかればいいんじゃないかと、教えてきたことを紹介します。
普通では考えないことをイメージするから難しい
2㎝は8㎝の何倍?
2㎝は8㎝の何割?
2㎝は8㎝の何%?
これは全部同じことを問いていることになりますね。
2㎝は8㎝の0.25倍
2㎝は8㎝の2割5分
2㎝は8㎝の25%
基本的な計算は、2÷8=0.25なのですが、この計算式になることの前に、わかってほしいことがあるのですが、それがわかりにくいというか、どうして?どうして?がいつも起こるのが、割合ですね。
この計算ができるというか、この問題をスラっと解けるようになることが割合の理解到達度として目標にしてほしいと思います。
使えるスキルとして、割合はこれができればいいと思っています。
これ以上のレベルのぐちゃぐちゃした文章問題なんかは、文章理解が重要なので、捨ててもいいと私は思っています。
まず、この基本的な問いを確実に理解できるようにすることがポイントだと思います。
割合を難しくしている割合の表し方を乗り越えよう
考えることと覚えることはちょっと別なことだと思いますから、割合で確実に覚えないといけないことは徹底的に覚えてもらいましょう。
それは、百分率などの表し方です。
あらわし方は、
- 割合の表し方
- %表示(百分率)
- 歩合
これは、表にしてあらわして覚えてもいいのですが、割合の1と1割を混同する子どもがいますから、そこは、野球の打率、そば粉の割合、飲料の百分率表示などを活用しましょう。
- 1=10割=100% → 1=100%=10割
- 0.1=1割=10% → 0.1=10%=1割
- 0.5=5割=50% → 0.5=50%=5割 ※矢印のあとの並びのほうが理解しやすいかも
を確実に理解させ、
- 0.01=1%=1分
- 0.001=0.1%=1厘
を理解させましょう。
割合はすべて「倍」のことだととらえてもらいましょう
そもそも、算数の問題自体が普通では考えないような問いになっているからだと私は個人的に思います。
このわかりにくさをわかりやすくするために、割合では、もとにするものを1と考えますね。
もとになるものを1つ分として、比べてみる。これが割合のはじめの一歩でもあると思いますが、これが誰にでもスンナリいかない。
上の問題が、例えば、8㎝は2㎝の何倍となると、2㎝の4つ分だから、4倍とすぐにわかる。2×4=8だからと考える子も多い。
考えやすいということは、イメージしやすいということだと思います。
だいたい、8㎝と2㎝を比べる状況で、2㎝の4倍が8㎝とか8㎝の4分の1が2㎝とかそういうイメージではないかと思うのです。
もとがどれとか、比べらえるものがどれということばかりに注目させないで、次のように、物事の流れでイメージさせてみてはどうかと、取り組ませました。
100万円をもとに考えてみると、
100万円の100%は100万円
100万円の全部は100万円
これは誰でもわかる。
100万円の2倍は200万円
100万円の1倍は100万円
100万円の0.5倍は50万円
100万円の50%は50万円
100万円の30%は30万円
1万円の0.2倍は2000円
500グラムの半分は250グラム
こういう問題を徹底的にやらせます。100万円は100なので楽なのですが、数値を変えて、考えさせます。
これは、かけ算になっていることは、「~の倍は」という文言があるので、わかるでしょう。でも、そのままでは気づけないので、
割合の数値(整数や少数、分数)は、すべて倍としてとらえていいことを教えます。
「割合は、何倍になっているかということでもある。」ことを基本的にとらえさせます。
ただし、倍としてとらえていいのは、割合にした時の整数・少数(分数)だけ。
百分率や歩合をそのまま倍としてとらえてしまう子どもが多いので、重要です。
これだけわかれば割合の問題は簡単に解ける【基礎編】
割合の問題はかけ算の式になる
次のような問題があります。
- 合唱部の希望者は20人で, 定員の0.4倍にあたるそうです。定員は何人ですか。
この文章から、○○は、□□の何倍 という部分を探します。
合唱部の希望者は20人で, 定員の0.4倍にあたるそうです。定員は何人ですか。
というふうに、取り出せます。
これを式にしてしまいます。
希望者 は 定員 の0.4倍 の文で、「は」→=のこと、○○の何倍→かけ算(×)に直します。
希望者 = 定員 ×0.4 となります。
希望者は20人となっていますから、
20=□×0.4 という式になりました。
これを解けばいいのです。
このかけ算は、割り算で解けることをわからなければ、以下のように説明しましょう。
6=□×3 という場合、□はどうやって解くか?
二三が六の九九でわかるのですが、6÷3=2ですから、これと同じように考えて、
20÷0.4=50ということがわかると思います。
割合の問題は、そのほとんどが文章で問いてきます。その文章から、
○○は、□□の何倍 という部分を探すことができれば、式にして、それを解くだけです。
ただし、これは、文章を正しく言葉を拾う必要がありますから、練習は必要です。
文章から式を見つけ出すためには練習あるのみ
- 赤いリボンが1.8mあり, 青いリボンは赤いリボンの1.5倍あります。青いリボンの長さは何mですか。
青いリボン=赤いリボン×1.5 → 青いリボン=1.8×1.5
- バスケットボールの値段は2800円で, これはバレーボールの1.4倍にあたるそうです。バレーボールは何円ですか。
これ=バレーボール×1.4 → 2800=バレーボール×1.4
これというものがバスケットボールの値段の2800円を指していることを読み取れない子どももいますから、基礎的な国語力はどうしても必要です。
だから、文章を読み取るだけの練習でもいいのでやらせましょう。
- 書道部の希望者は21人で, 定員の140%にあたるそうです。定員は何人ですか。
素直に読み探せないような位置にある言葉をちゃんとあてはめないと日本語が合わなくなりますから、読み取り練習は必要ですね。
これは、百分率で割合をあらわしていますから、割合の数値に直さないと計算に使えません。
140%は、1.4になり、
希望者=定員×1.4 → 21=定員×1.4 となりますね。
- こころさんは, バスケの試合で16回シュートして10回シュートを決めました。成功した回数は, シュートした回数の何割ですか。歩合で表しましょう。
成功した回数=シュートした回数×□
何割というのは、倍と同じに考えていいから、何倍ということです。
成功した回数が10回 シュートした回数が16回となっていますから、
10=16×□ → □=10÷16 となりますね。
これも 割り算で□がわかるのですが、どちらをどちらで割るかについては、12=4×□で考えさせましょう。
こんなふうに、ドリル的に問題になれて、文章の読み取りに慣れていくことで、割合の問題を解く方法が身につきます。
もちろん、これで割合の問題が全て解けるようになるのは、ちょっと無理ですね。
この基本レベルの次は、割引などの問題が出てくるわけです。
この割引きの問題も実は、文章の読み取りができれば、そんなに難しいことではないのですが、その読み取りが小学生や中学生にはかなり難解となる文章なのです。
割引の問題がすらすら解けるようになるには、文章を読む力がないと無理なので、割引問題については、次回でお話します。
まとめ
割合の問題は、かけ算で考えるという方法をお話しました。
割合は、何倍になっているかということです。
算数の問題はわかりにくいものが多く、それを解けるようになるには、やはり練習するしかありません。「できたで終わらせないで、どんどんできたにする」には、どうしても練習あるのみだと私は思います。
勉強が苦手な子どもにとっては、教科書通りにやってもなかなか理解してもらえません。
こうすれば解けるということを子どもたちにどんどん教えていいと思います。ここで紹介したことが一番いい方法とは言えませんし、この方法でなくても理解できる子どもはそれでいいと思います。
本当にできない子どもには、そういうことか!という納得が特に必要です。教科書のことがわからなくても、割合の何かしらが理解出来たらいいと思います。
稚拙な内容でしたが、参考になれば有難いです。
算数難しい割合!小学5年算数割合の問題はこう考えよう⁉解き方と教え方についてのお話でした。最後までお読みいただきありがとうございました。


コメント